Statistics: Variables

Types of Variables

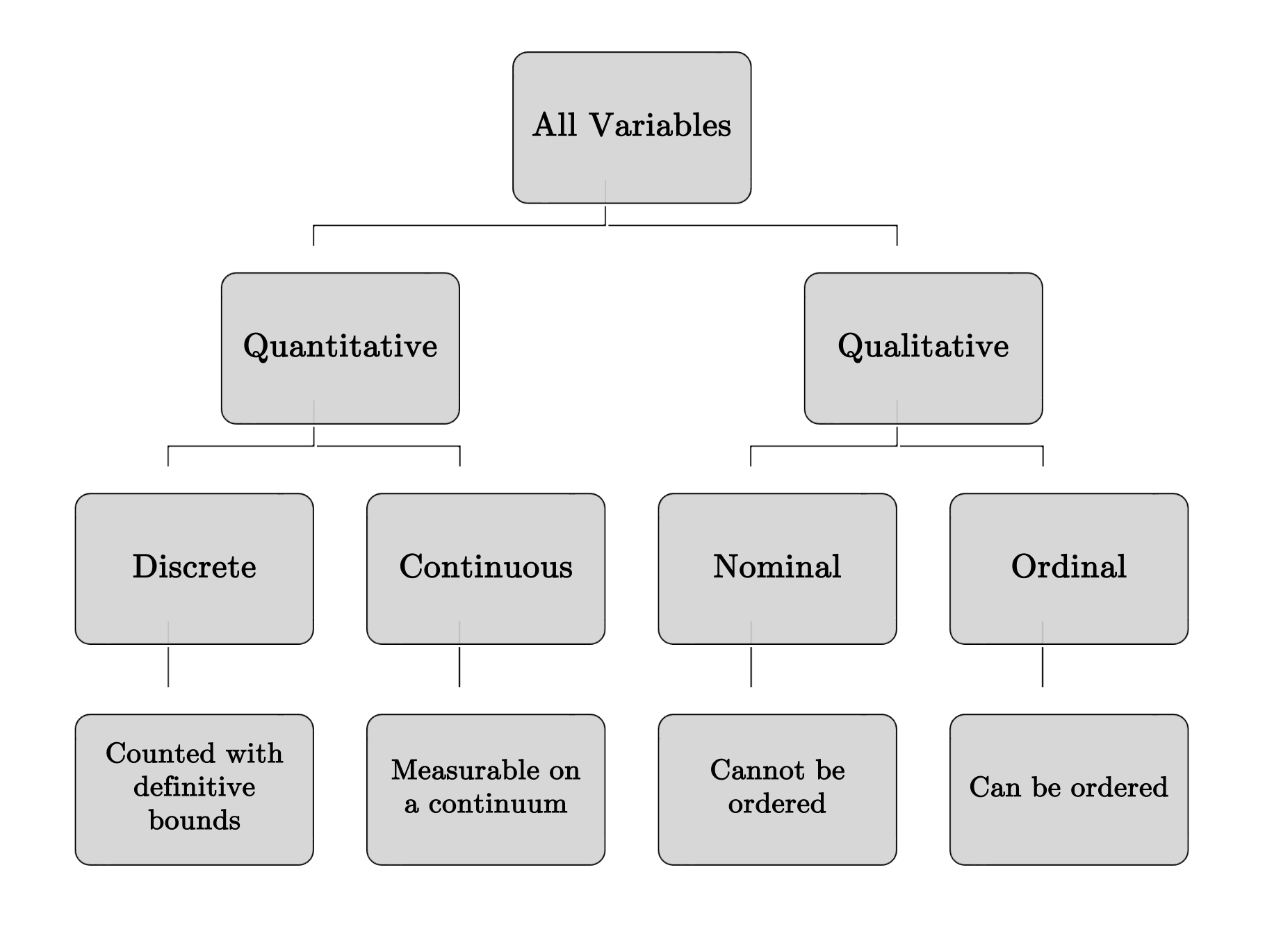
In statistics, data is classified based on the type of variable being measured. Understanding the types of variables is essential as it dictates the appropriate statistical methods for analysis. Variables can broadly be categorized into quantitative (numerical) and qualitative (categorical) types, with further subdivisions.

Quantitative Variables

Quantitative (numerical) variables represent numerical data that can be measured and ordered. These variables convey information about quantities or amounts and can be analyzed using mathematical operations.

Quantitative variables can be further classified into two types:

• Continuous Variables:

  • Continuous variables can take any value within a range and can be infinitely divided. For example, height, weight, or temperature can take on any value (e.g., 5.5 feet or 68.2 degrees Fahrenheit).

  • Example: The height of students in a class.

• Discrete Variables:

  • Discrete variables take specific, countable values. These are usually whole numbers or fixed units, and cannot be subdivided into smaller units meaningfully.

  • Example: The number of cars owned by a household (e.g., 0, 1, 2, 3, etc.).

Qualitative (Categorical) Variables

Qualitative (categorical) variables represent categories or characteristics rather than numerical values. These variables describe qualities or labels of the entities being studied.

Qualitative variables can be divided into two types:

• Nominal Variables:

  • Nominal variables represent categories that have no natural ordering or ranking between them. These are purely labels or names.

  • Example: The type of car (e.g., sedan, SUV, truck).

• Ordinal Variables:

  • Ordinal variables represent categories that have a natural order or ranking, but the intervals between the values may not be equal. While you can rank the data, the difference between the ranks may not be consistent or meaningful.

  • Example: Satisfaction levels in a survey (e.g., “very dissatisfied,” “dissatisfied,” “neutral,” “satisfied,” “very satisfied”).

Other Particular Types of Variables

Binary (Dichotomous) Variables

A binary variable is a type of qualitative variable that has only two possible categories or values. These variables are often coded as 0 and 1 in statistical analysis.

• Example: Gender (male/female), whether a person owns a car (yes/no).

Interval Variables

Interval variables are numerical variables where the difference between values is meaningful, but there is no true zero point. This means that ratios between numbers are not meaningful, but the difference is.

• Example: Temperature in Celsius or Fahrenheit (e.g., 20°C is not twice as hot as 10°C, but the difference between 20°C and 10°C is meaningful).

Ratio Variables

Ratio variables are like interval variables, but with a meaningful zero point, which allows for the calculation of ratios. This means that you can make meaningful statements about how many times larger one value is compared to another.

• Example: Income, weight, and height. A person who earns \(100,000 earns twice as much as a person who earns \)50,000.

Summary of Variable Types

Variable Type	Description	Examples	Level of Measurement
Continuous	Can take any value within a range (infinitely divisible).	Height, weight, temperature	Quantitative (Numerical)
Discrete	Takes specific, countable values.	Number of students, number of cars	Quantitative (Numerical)
Nominal	Categories with no natural ordering.	Gender, car type, country of residence	Qualitative (Categorical)
Ordinal	Categories with a natural order or rank, but unequal intervals.	Education level, satisfaction level	Qualitative (Categorical)
Binary	Two possible categories.	Yes/No, Male/Female, True/False	Qualitative (Categorical)
Interval	Numeric data with meaningful differences, but no true zero.	Temperature (°C, °F), IQ scores	Quantitative (Numerical)
Ratio	Numeric data with a meaningful zero point, allowing for ratios.	Income, height, weight	Quantitative (Numerical)

Random Variables

Where randomness is a bedrock characteristic for inferential statistics, many variables we will encounter are random variables, or variables where possible outcomes are numerical outcomes of a random phenomenon.

Note: Because RVs capture numerical outcomes, they are either discrete or continuous.